Finding Volume with Calculus

There are three methods to calculate/estimate the volume of an object:

1. General Slicing Method: given the base, and assumption that every perpendicular slice are simple shapes and similar to each other.
2. The Disk Method: given the outline of the shape that revolves around an axis.
3. The Shells Method: break the structure down into layers, similar to an onion. Often used when the two methods above cannot be applied.

The following parts will discuss in detail the three methods.

General Slicing Method

This method is used when there is a base, and the perpendicular intersections are similar simple shapes.

Example 1: Find the volume of the parabolic cube. The base is the parabola $y=1-x^2$ in the first quadrant. The perpendicular intersections are squares.

Remember not to limit yourself when sketching the graph.

Example 2: Find the volume of the semi-circle cube. The base is a semi-circle with the radius of 6. The perpendicular intersections are squares and are parallel to the diameter of the semi-circle.

When solving this problem, I fell into the trap of graphing the semi-circle on the second and third quadrant. This prevents me from iterating along the x-axis. In this problem, of course it is easy to switch the axis and iterate along the y-axis, but why spare the time to do that when you can graphic differently.

The Disk Method

This method is used when the 3D object can be easily be broken down into layers of dish, often when a simple graph revolves around an axis. Be aware that an axis can be any axis, such as the x-axis, the $x=-5$ line may also be used as a axis, but a curve is not an axis!

Example 1: Find the volume of the 3D shape made by rotating the function $y=(x+1{)}^2$ around the x-axis. The bounds are $x=0$ and $x=2$.

When there are two function involved, note that you cannot rotate a function around a curve, or a diagonal line, which is usually the other function.

Example 2: Given the two functions $f(x)=\sqrt{x}$ and $g(x)=x^2$, line $x=0$ and $x=1$. Find the volume of the object made by rotating the two functions around the x-axis.

The Shells Method

The Shells Method comes in handy when the above two methods make solving the problem troublesome. Take a look at this example:

R is the region in the first quadrant bounded by the graph $y=x^2-x^3$ and the x-axis. When R is revolved about the y axis, the resulting solid has a volume that is difficult to compute with the disk method.

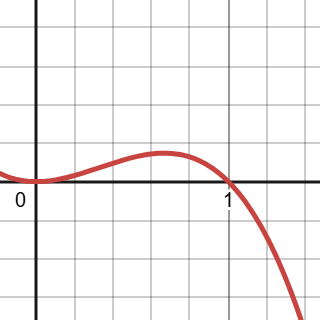
So imagine the solid created is an onion, which has many different layers. We are going to unravel the onion, and calculate the volume of each layer. With calculus, we can cut the onion into so many layers that we only need to calculate the area of each layer. That is the shells method.

$f(x)$ is the function above, $g(x)$ is the function below. $a$ and $b$ are the two bounds. We have a general equation:

$$V={\int }_b^{a}2\pi x(f(x)-g(x))dx$$

Note that $2\pi x$ is the shell circumference. It is $x$ because we are assuming that the bounded region is revolving around the y-axis. If revolving around a different axis, the circumference is $2\pi \text{(distance from the axis)}$. The $(f(x)-g(x))$ is the height of each cell.

My note may make it unclear for some reader. I’m trying my best to simplify while retaining mathematical accuracy of my note; however, I recommend reading from other sources to demystify this topic.