06 Work and Kinetic Energy

Work

While the object moves, a constant force $\vec{F}$ acts on it in the same direction as the displacement $\vec{s}$. We define work done by this constant force under these circumstances as the product of the force magnitude $F$ and the displacement magnitude $s$.

$$W=Fs\text{ (constant force in direction of straight-line displacement)}$$

Caution

Do not confuse $W\text{ (work)}$ with $w\text{ (weight)}$. Work done can be positive, negative, or zero.

The SI unit of work is $\text{joule}$. Note that $1J=1N.m\text{ (newton-meter)}$.

When applying the work formula into an $\text{x-y plane}$, use this formula:

$$W=\vec{F}\cdot \vec{s}=F\times s\times \cos \varphi$$

Where $\varphi$ is the angle between the displacement and the force. Remember that work is a scalar quantity, meaning that it does not have any direction.

When you have individual elements of a vector instead of the angle between the two vector, you can do this instead:

$$W=\vec{F}\cdot \vec{s}=F_{x}x+F_{y}y\text{ and so on}$$

Kinetic Energy and Work-Energy Theorem

Deriving the formula for Kinetic Energy:

$$v_2^2=v_1^2+2a_{x}s$$ $$a_x=\frac{v_2^2-v_1^2}{2s}$$ $$F=m{a}_x=m\frac{v_2^2-v_1^2}{2s}$$ $$Fs=\frac{1}{2}m{v}_2^2-\frac{1}{2}m{v}_1^2$$

Note that $Fs$ is the total work $W_{tot}$ done by all of the forces acting on the particle. The quantity $\frac{1}{2}m{v}^2$ is called $\text{kinetic energy K}$ of the particle. Fancy.

$$K=\frac{1}{2}m{v}^2$$

Kinetic is also a scalar quantity and depends only the particle mass and speed, not its direction of motion or the net force. Kinetic energy is also never negative, and is zero when the particle is at rest. This make working with kinetic energy to derive work is a lot more easier.

We have the Work-Energy Theorem:

$$Fs=W_{tot}=K_2-K_1=\Delta K=\frac{1}{2}m{v}_2^2-\frac{1}{2}m{v}_1^2$$

The SI unit for Kinetic Energy is $kg\cdot (m/s{)}^2\text{ or }kg\cdot m^2/v^2$.

With the work energy theorem, we have a connection between the force, the displacement, the mass, and the initial, final velocity.

Work done by a varying force, straight line motion

Until now, we have only worked with constant forces, because we fear the integrals. Now, let’s work with the integrals.

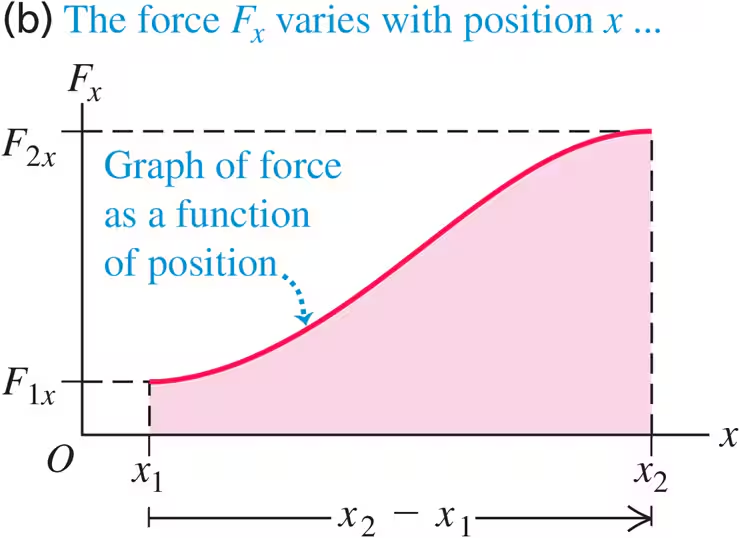Look at this beautiful graph, we can calculate the area under the curve by using integrals.

$$W={\int }_{x_1}^{x_2}{F}_{x}dx$$

This is especially helpful when we apply the work-energy theorem to the spring, because the more you pull or push a spring, the harder it gets. This follows Hooke’s law (more like a statement of an ideal spring):

$$F=kx$$

Where $k$ is the spring constant. We can calculate the total work using the previous formula:

$$W={\int }_0^{X}kxdx=\frac{1}{2}k{X}^2$$

Power

Power is the time rate at which work is done. Like work and energy, power is a scalar quantity:

$$P_{av}=\frac{\Delta W}{\Delta t}$$

The instantaneous power, or the rate of work can be calculated as:

$$P=\underset{\Delta t\to \infty }{\lim }\frac{\Delta W}{\Delta t}=\frac{dW}{dt}$$

The SI unit for power is watt $(W)$. $1W=1J/s$.

In mechanics, we can also express power in terms of force and velocity.

$$P=\vec{F}\cdot \vec{v}$$