Rocket launch problem

A rocket, initially at rest on the ground, accelerates straight upward from rest with constant (net) acceleration $44.1{\text{m/s}}^2$ . The acceleration period lasts for time $9.00s$ until the fuel is exhausted. After that, the rocket is in free fall.

Find the maximum height $y_{max}$ reached by the rocket. Ignore air resistance and assume a constant free-fall acceleration equal to $9.80{\text{m/s}}^2$ .

Given:

• Net acceleration $a_0=44.1{\text{m/s}}^2$
• Acceleration lasts for $t=9.00s$
• Free-fall acceleration $g=9.80{\text{m/s}}^2$

Find: The maximum height reached by the rocket.

Theory:

• $x=x_0+v_{0}t+\frac{1}{2}{a}_x{t}^2$
• $x-x_0=\frac{1}{2}(v_{0x}+v_x)t$
• $v_x^2=v_{0x}^2+2a_x(x-x_0)$

Assumption:

• The rocket accelerates upwards with the same acceleration of $a_0=44.1{\text{m/s}}^2$ until the fuel runs out.
• After the fuel runs out, the rocket still ascends upwards but with $g=9.80{\text{m/s}}^2$ downwards.

Graph: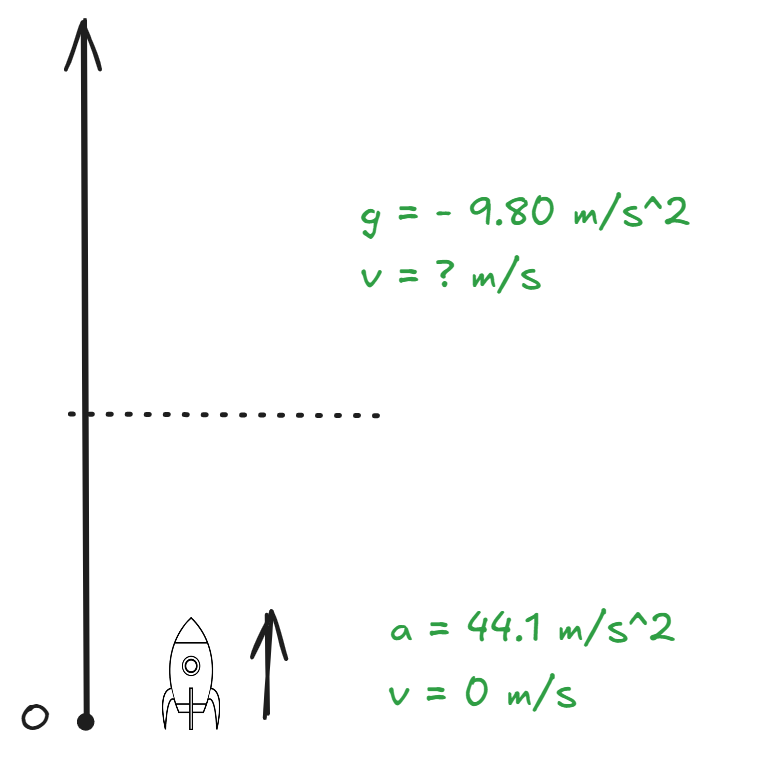

Solution:

The first part: The rocket ascends until the fuel runs out

• $x_0=0\text{ m}$
• $v_0=0\text{ m/s}$
• $a=44.1{\text{ m/s}}^2$
• $t=9.00s$

The height the rocket reaches before the fuel runs out

$$x=x_0+v_{0}t+\frac{1}{2}a{t}^2$$ $$x=0+(0)9.00+\frac{1}{2}(44.1)(9^2)$$ $$x=1.79\times 10^3\text{ m}$$

When the fuel runs out, the rocket has the velocity of:

$$x-x_0=\frac{1}{2}(v_0+v)t$$ $$1.79\times 10^3-0=\frac{1}{2}(0+v_x)(9)$$ $$v_x=396.9\text{ m/s}$$

The rocket keeps ascending until the velocity is zero and start free falling:

$$v_x^2=v_0^2+2g_{}(x-x_0)$$ $$0=(396.9^2)+2(-9.80)(\Delta x)$$ $$\Delta x=8.04\times 10^3\text{ m}$$

Then the total height the rocket reaches is $9.83\times 10^3\text{ m}$